- 01 de Octubre del 2015:

En nuestro primer día de clases abordamos el tópico de los números complejos, demostrando su notación, la representación algebraica, binomica y cartesiana; y cuales son los posibles usos respecto al caso que estudiemos. Ademas realizamos las demostraciones correspondientes a las operaciones con números complejos: suma, resta, multiplicación y división.
Vimos la definición del conjugado de z. La cual solo difiere por el signo negativo a la parte imaginaria del numero. De igual manera el módulo de z y las propiedades del conjugado y el módulo de un complejo.
Para mayor información se proveen de las siguientes fuentes bibliográficas:
- 05 de octubre del 2015:


Las potencias y raíces de los números complejos, se deben trabajar de la siguiente manera con su modulo y argumento del mismo. Verificando los signos del argumento y periodicidad en la cuestión de las raíces.
La Fórmula de Euler, nos presenta una mayor manejo del numero complejo debido a su forma exponencial antes que la forma convencional del Cis del argumento o mejor dicho la forma trigonométrica o polar de un complejo la cual presenta un mayor grado de dificultad en el manejo de ejercicios antes que la forma de Euler.
Para mayor información se proveen de las siguientes fuentes bibliográficas:
- 08 de octubre del 2015:

Realizamos varios ejercicios prácticos y sencillos y notamos la definición de la distancia entre dos números complejos y la representación de un círculo y recta en el plano complejo este ultimo tópico presenta cuestiones de análisis respecto al conjunto del plano en cuestión que estamos trabajando debido que debemos analizar en un intervalo cerrado en cuestión al circulo que definamos en el plano de los complejos.
Para mayor información se proveen de las siguientes fuentes bibliográficas:http://www.vitutor.com/di/c/ejercicios_complejos.html
http://www.dynamics.unam.edu/NotasVarias/NotasVC.pdf
- 12 de octubre del 2015:
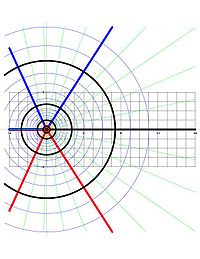

Al igual que en el plano de los reales existen funciones de la misma manera existe en el plano complejo, las funciones de variable compleja y su representaciones gráficas a partir de un plano real a un plano complejo (Transformaciones del plano complejo) y por ultimo tenemos los Límites en los números complejos, que presentan una gran similitud en la resolución de los limites al igual que en los números reales.
Para mayor información se proveen de las siguientes fuentes bibliográficas:http://www2.caminos.upm.es/Departamentos/matematicas/Fdistancia/PIE/Analisis%20matematico/Temas/C02_Funciones_complejas.pdf
http://www.ma.uva.es/~antonio/Teleco/Apun_Mat2/2_Tema-9.pdf
- 15 de octubre del 2015:
Primera prueba del primer bimestre.
- 19 de octubre del 2015:

Abordando después de la prueba el tema en limites de números complejos tomamos en cuenta las siguientes definiciones Continuidad, Discontinuidad y Derivación.
En continuidad cumplen los mismos requisitos en el plano de los reales al igual que en la discontinuidad; mientras que en la derivación de numero complejos se asemeja mucho a los números reales pero se deben tener varias consideraciones al momento de derivar en el caso del complejo de un numero conjugado.
Para mayor información se proveen de las siguientes fuentes bibliográficas:http://es.slideshare.net/marvinconcha1901/2do-trabajo-de-matemtica-aplicada-ii-limites-y-continuidad-en-complejos-untecs
http://corcoles.org/uoc/anmat/es/es32.xml
- 22 de octubre del 2015:
IV jornadas de ingeniería civil y ambiental.

- 26 de octubre del 2015:


La implementacion de las ecuaciones de Cauchy - Riemann, para las resolución de varios casos es necesaria tomando en cuenta las derivadas parciales de la funciones en el caso de estudio y sus segundas derivadas. La definición de las Funciones analíticas y las restricciones que deben tomar en cuenta para que cumpla con la definición al no tener ningún tipo de restricción en el dominio de la función y por ultimo la definición de Funciones armónicas la cual se obtiene cunado las segundas derivadas parciales sean iguales.
- 29 de octubre del 2015:


Al fin de mes realizamos un repaso general de las Funciones trascendentes básicas: exponencial, logarítmica, trigonométricas, hiperbólicas; y las consideraciones que se deben tomar en cuenta para la resolución de las mismas en los números complejos. Se introdujo la definición de logaritmos en los números complejos. Y realizamos varios ejercicios en clase.
Para mayor información se proveen de las siguientes fuentes bibliográficas:http://www.ditutor.com/funciones/funcion_trascendente.html
http://fernandorevilla.es/blog/2014/08/06/funciones-trigonometricas-complejas/
No hay comentarios:
Publicar un comentario